Pregunta de: Probabilidad y Estadística
En un laboratorio se tiene en observación un conjunto de plantas que se estima presenta una extraña característica genética con probabilidad de 0.7. Para realizar un análisis se eligen 5 plantas al azar y se define la variable aleatoria X, la cual indica el número de plantas que presentan la extraña característica.
Determine la probabilidad de que en la elección la planta 3 presente dicha característica.
Considere para su cálculo la fórmula de la función de distribución:
0.132
0.308
0.343
Soluciones
Aún no hay soluciones para esta pregunta. ¡Sé el primero en agregar una!
Agregar una solución
No te pierdas la oportunidad de ayudar a los demás. ¡Regístrate o inicia sesión para agregar una solución!
Demuestra tu conocimiento
Ayuda a la comunidad respondiendo algunas preguntas.
La tabla muestra la distribución de frecuencia del número de …
La distribución del ingreso diario por familia de una pequeña …
En un estudio de mercado se registra la cantidad de …
Determine la moda de los datos obtenidos en un estudio …
Una propiedad de la curva de la distribución normal es …
Calcule el percentil 30 de los datos. 0.8, 1.2, 1.5, …
Un diseñador terminó de elaborar 1 cartel y tiene disponibles …
Identifique el tipo de frecuencia presentado en la columna z. …
Calcule la varianza de la cantidad de alumnos encuestados en …
¿En cuál de los siguientes gráficos se utiliza una medida …
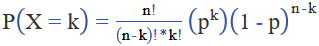
Exani