Pregunta 1 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Seleccione el valor del límite en la siguiente función.
lim x → -2 de 2x3 + 2x2 + 2
-22
-6
26
Pregunta 2 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Calcule la distancia en metros que recorre en los primeros 4 segundos una piedra que se arroja desde un edificio si ésta tiene en el instante t = 0 una velocidad de v = 9.8 t + 8.
9.8
51.6
110.4
Pregunta 3 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Identifique la función que se resuelve como integral inmediata mediante manipulación algebraica.
∫ x5 + 2 dx
∫ (x + 2)5 dx
∫ x(x + 2)5 dx
Pregunta 4 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Calcule el valor del límite en la función.
limx → ∞ 3 - 6x2 / 5x + 9x2
-3 ⁄ 9
-2 ⁄ 3
-3 ⁄ 2
Pregunta 5 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Determine el área encerrada por la función f(x) = 4 - x2 y el eje x.
16/3 u2
32/3 u2
48/3 u2
Pregunta 6 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Identifique la integral de la función ∫x√(x + 1) dx a partir de la integración por partes.
Pregunta 7 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Calcule la integral de la función exponencial.
∫5x dx
5x + C
5x/5+C
5x/ln 5+C
Pregunta 8 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Seleccione la ecuación de la recta tangente a la gráfica de la función f(x) = 3x2 + 4 en el punto P(1, 7).
y=6x+1
y=6x-41
y=7x+0
Pregunta 9 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
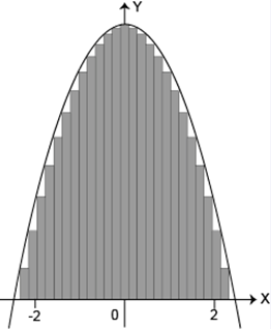
Identifique la partición que más se aproxima al área bajo la curva.
Pregunta 10 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Calcule la integral de la función trigonométrica.
∫sen32x dx
Pregunta 11 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Seleccione el límite de la función f ( x ) = 9x2 + 12x + 3 , por medio del cual se obtiene la derivada por definición.
lim x → x0 ( (9x2 + 12x + 3) - 9x02 + 12x0 + 3 ) ⁄ (x - x0)
lim x → x0 ( (9x2 + 12x + 3) - (9x02 + 12x0 + 3) ) ⁄ (x - x0)
lim x → x0 ( (9x02 + 12x0 + 3) - (9x02 + 12x + 3) ) ⁄ (x - x0)
Pregunta 12 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Identifique la derivada de la función.
f ( x ) = e x6
ex6
6x5ex6
6x6ex6
Pregunta 13 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
La relación entre la distancia recorrida en metros por un móvil y el tiempo en segundos es s ( t ) = t ( 1 . 5 t - 2 ). ¿Cuál es la velocidad instantánea que lleva el móvil a los 4 segundos?
10 m/s
12 m/s
16 m/s
Pregunta 14 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Relacione cada propiedad de los límites con la solución correspondiente para dos funciones f(x) y g(x) cuyos límites existen.
| Propiedad |
Solución |
| 1.- Producto |
a) lim x → c b[ f ( x ) ] = b lim x → c f ( x ) |
| 2.- Cociente |
b) lim x → c [ f ( x ) g ( x ) ] = lim x → c f ( x ) - lim x → c g ( x ) |
| 3.- Multiplicación escalar |
c) lim x → c ( f ( x ) / g ( x ) ) = ( lim x → c f ( x ) ) / ( lim x → c g ( x ) ) |
1a, 2c, 3b
1b, 2c, 3a
1c, 2b, 3a
Pregunta 15 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Identifique la sustitución que ayuda a resolver la integral de la función.
∫ 2 / √(6 - 6x2) dx
x = sec α
x = tan α
x = cos α
Pregunta 16 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Identifique la derivada de la composición f(g(x)) considerando las siguientes funciones.
f(x) = √(x)
g(x) = x3 + 3x2 + 1
Pregunta 17 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
¿Qué propiedad se utiliza para resolver la siguiente integral?
∫12 (x + 1) dx
∫ba f(x) dx = -∫ab f(x) dx
∫ba f(x) dx = ∫ab f(x) dx
∫ba kf(x) dx = k ∫ba f(x) dx
Pregunta 18 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Calcule el valor de la integral definida de la función.
∫14 (x2 + x) dx
-171 ⁄ 6
171 ⁄ 6
181 ⁄ 6
Pregunta 19 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
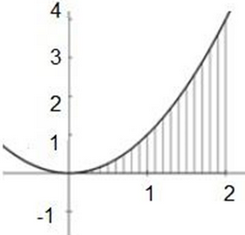
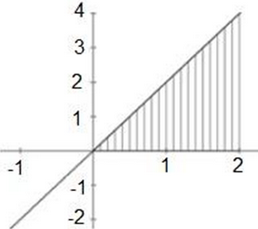
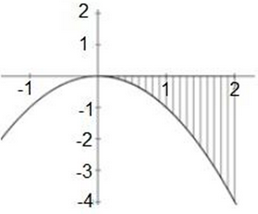
Seleccione la gráfica que refleja la resolución de la integral.
∫02 2x dx
Pregunta 20 de 20
Exani II -> Módulos Específicos -> Cálculo Diferencial e Integral
Calcule la derivada de la función polinomial.
f(x) = x3 + 4x2 + 2x - 7
3x2 + 8x
3x2 + 8x + 2
3x2 + 8x + 2 - 7
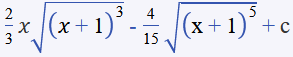
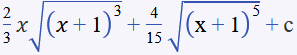


 Exani
Exani